back in the (former) USSR

Here's another post inspired by some initial exchanges over on Twitter - it also shares a theme with this earlier post about imaginary straight-line journeys between American states. I follow a few map-related accounts on Twitter and one of them tweeted the map below which I quote-tweeted with a challenge, also related to imaginary straight-line map journeys, as you can see:

Interesting academic challenge: given a free hand to select any two distinct points in a country, can you select two so that a straight line between them passes through the maximum number of other countries? And, given the whole world to play with, what is that maximum number? https://t.co/BFYDthfqYk

— Dave Thomas (@electrichalibut) November 23, 2021

You can see, just at a conceptual level, the sort of thing we'll be looking for here: quite large countries which have fairly irregularly-shaped borders, in particular we're looking for areas of convexity where you can draw a line which joins two points in the country but passes outside of it in doing so. As you'll see from the thread following that initial tweet, I had a go at finding a few - examples are below:

Uzbekistan - Kazakhstan - Tajikistan - Kyrgyzstan - Uzbekistan:

Brazil - Colombia - Venezuela - Guyana - Suriname - French Guiana - Brazil:

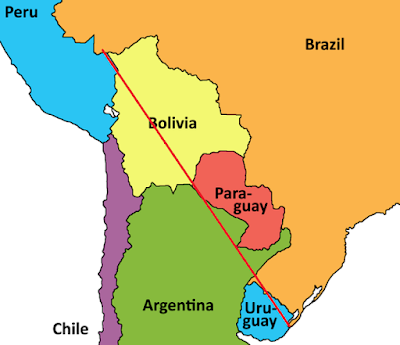
Brazil - Peru - Bolivia - Paraguay - Argentina - Uruguay - Brazil:

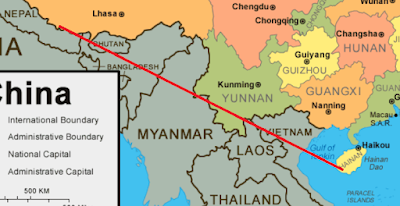
China - Nepal - India - Bhutan - Myanmar - Laos - Vietnam - China:

Democratic Republic of the Congo - Uganda - Rwanda - Burundi - Tanzania - Zambia - Democratic Republic of the Congo:

All of those (apart from the first one) traverse five other countries (in some cases more than once, and in some cases re-entering itself - ooer - on the way; I deem this not to matter) before coming back into the starting country. Better ones are available, and it should come as no surprise that the best one I know of (and it wasn't my work, I should add) features the largest country in the world, Russia. This one starts on the western edge of the Caspian Sea and then traverses no fewer than eight other countries before returning to Russia over near Vladivostok. Take a look:

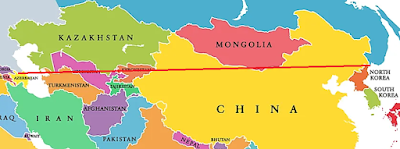
Russia - Azerbaijan - Turkmenistan - Kazakhstan - Uzbekistan - Kyrgyzstan - China - Mongolia - North Korea - Russia:

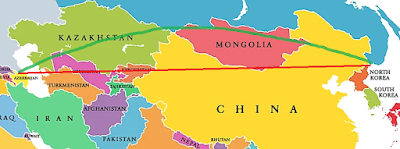
Now I know what you're thinking: a pity we couldn't juuuuust bend the line southwards slightly to snick the top end of Tajikistan as well, as that would clock up an extra country. This is dangerously subversive thinking and opens up questions like: you know, the world is not actually flat, so doesn't this whole straight line thing depend entirely on which map projection you're using? And my answer to that is WELL I'M GLAD YOU ASKED as there is a whole other world of nerdy interest there which there isn't really time and space (if you will) to go into now. Suffice it to say that the only projection-independent way of rendering straight lines is to use great circles, which look a bit weird and somewhat counter-intuitive on 2-dimensional maps given that they actually represent the shortest distance between points on the Earth's surface (assuming you're constrained to travelling over that surface rather than just tunneling directly through the Earth's crust). A great circle route between our Russian end-points actually reduces the country count considerably, as it looks like this:

Represented on the original map 2-D that would look something like this (the green curved line) - note that this way you lose Turkmenistan and Kyrgyzstan from the original list:

The borders between Kyrgyzstan, Tajikistan and Uzbekistan are actually even more complex and wiggly and convoluted than this fairly large-scale map makes it look, as it happens. We might come back to this later. 

Anyway, I leave you with the words of TS Eliot which seem somehow appropriate here:

And the end of all our exploring

Will be to arrive where we started

And know the place for the first time